BAGS is a fortnightly seminar at the University of Bath on Arithmetic Geometry with a view towards rational points; run by Julian Lyczak and Harkaran Uppal.
Location: The Wolfson Lecture Theater, Building 4 West, University of Bath
Date & Time: Every other week on Tuesday, 15:15 - 16:15.
| Date | Speaker | Affiliation | Title |
|---|---|---|---|
| Oct 3rd | Rachel Newton | King's College London |
Counting S4 and S5 extensions satisfying the Hasse norm principleAbstract: Let L/K be an extension of number fields. The norm map N_{L/K}:L*->K* extends to a norm map from the ideles of L to those of K. The Hasse norm principle is said to hold for L/K if, for elements of K*, being in the image of the idelic norm map is equivalent to being the norm of an element of L*. The frequency of failure of the Hasse norm principle in families of abelian extensions is fairly well understood, thanks to previous work of Christopher Frei, Daniel Loughran and myself, as well as recent work of Peter Koymans and Nick Rome. In this talk, I will focus on the non-abelian setting and discuss joint work with Ila Varma on the statistics of the Hasse norm principle in field extensions with normal closure having Galois group S_4 or S_5. |
| Oct 17th | Alex Torzewski | King's College London |
Studying points on varieties via varying familiesAbstract: We show how Lawrence-Venkatesh's method for studying points on a variety X can be applied to curves in families. In the process, we also outline the original method. The idea is that if there exists a family over X which varies "a lot", then this strongly constrains the existence of points. This is an example of how topology influences arithmetic, in this case via p-adic differential equations! |
| Oct 31st | Alec Shute | University of Bristol |
Zooming in on quadricsAbstract: Classically, Diophantine approximation is the study of how well real numbers can be approximated by rational numbers with small denominators. However, there is an analogous question where we replace the real line with the real points of an algebraic variety: How well can we approximate a real point with rational points of small height? In this talk I will present joint work with Zhizhong Huang and Damaris Schindler in which we study this question for projective quadrics. Our approach makes use of a version of the circle method developed by Heath-Brown, Duke, Friedlander and Iwaniec. |
| Nov 14th | Tobías Martínez | Universidad de El Salvador |
The Manin Conjecture for Hirzebruch-Kleinschmidt varietiesAbstract:In this talk, we will study Manin's Conjecture on certain projective bundles over projective spaces classified by Kleinschmidt (1988). To do so, we will analyze the analytic behavior of the height zeta function induced by a metrization on the anticanonical bundle, establishing a connection between this height and the norms of hermitian vector bundles over the arithmetic curve induced by the rings of integers of the underground number field. |
| Nov 28th | Adam Morgan | University of Glasgow |
Counterexamples to the Hasse principle in quadratic twist families of hyperelliptic curvesAbstract: In this talk I will discuss work in progress studying the number of counterexamples to the Hasse principle in quadratic twist families of hyperelliptic curves. In particular, I will sketch a proof that if g is at least 2, and f(x) in Z[x] is a squarefree polynomial of degree 2g+2 and Galois group S_{2g+2}, then there are infinitely many squarefree integers d for which the associated genus g hyperelliptic curve y^2=df(x) violates the Hasse principle. The argument uses results on the behaviour of Cassels—Tate pairings in quadratic twist families, in the spirit of recent work of Smith, and gives a lower bound for the number of such d that should be correct up to logarithmic factors. |
| Dec 12th | Samir Siksek | University of Warwick |
Galois groups of low degree points on curvesAbstract: Low degree points on curves have been subject of intense study for several decades, but little attention has been paid to the Galois groups of those points. In this talk we recall primitive group actions, and focus on low degree points whose Galois group is primitive. We shall see that such points are relatively rare, and that they interfere with each other. This talk is based on joint work with Maleeha Khawaja. |
On the campus of the University of Bath your goal is the building 6 West. Our offices are 6W 1.03 and 6W 1.27; they are directly on your left and right upon entering.
Bike:
The university is located upon a very steep hill. Cycling up is challenging for most people.
Bus from the city centre:
When you leave Bath Spa station you will want to cross the road and get the U1 bus up to uni (this stop is directly across from the bus station). Usually google maps calls this stop U1 Bus: Dorchester Street.
You will then want to get off at North Road. This will be the 10th stop after you get on the U1 at Bath Spa.
From there head to the building 6 West. To do this, take the left turning once you walk about 2 metres forwards after getting off the bus (the road is called soldier down lane). Keep going straight until the end of the road then take a left (this left should be slightly up hill). If you continue walking up this hill you should see a building with a big ramp leading up to it, this is 6 West. To get in just walk up the ramp through the double doors.
Here is the path (highlighted in blue) you can take.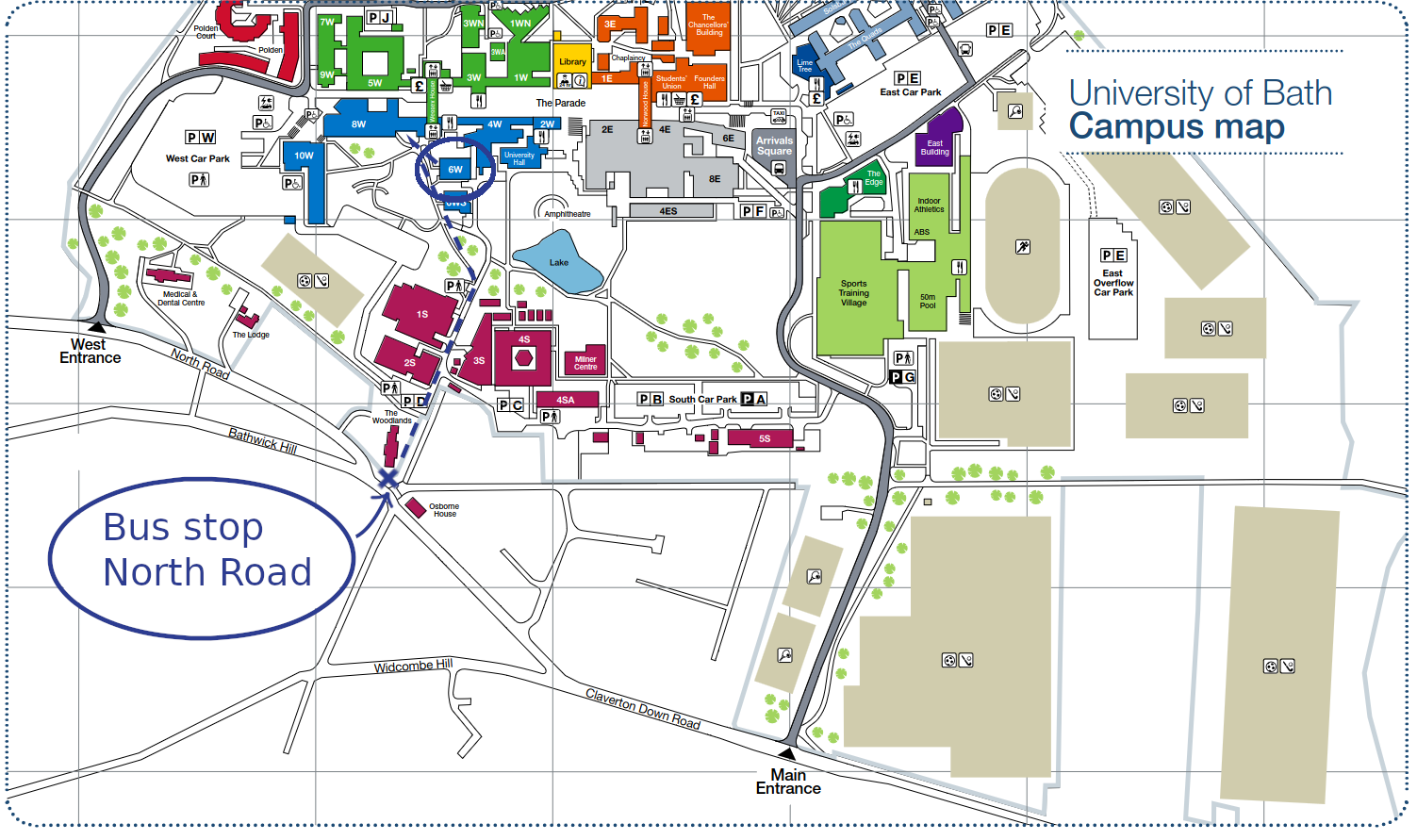
| Date | Speaker | Affiliation | Title |
|---|---|---|---|
| Jan 30th | Alexei Skorobogatov | Imperial College London | |
| Feb 13th | Martin Orr | University of Manchester | |
| Feb 27th | Tim Browning | IST Austria | |
| Mar 12th | Damián Gvirtz-Chen | University of Glasgow | |
| Mar 26th | |||
| Apr 9th | |||
| Apr 23th | |||
| May 7th | |||
| May 21st |